📝Light - Refraction
Refraction of light
When the light goes from air to glass, it bends towards the normal to the
interface separating these two media (fig a). On the other hand, when the
light goes from glass to air, it bends away from the normal to the interface
separating these two media (fig b). This phenomenon is known as the
refraction of light.

|
| (a) ∠i > ∠r |

|
| (b) ∠i < ∠r |
The bending of light rays when they pass obliquely from one medium to
another medium is called the refraction of light.
Cause of refraction of light.
A medium through which light can pass or transmitted is called a
transparent medium.
Every transparent medium has a property known as optical density. The optical density of a transparent medium is closely related to the speed of light
in the medium.
If the optical density of a transparent medium is low, then the speed of light in that medium is high. Such a medium is known as an optically rarer medium. Thus, an optically rarer medium is that medium through which light travels fast.
On the other hand, if the optical density of a transparent medium is high, then the speed of light in that medium is low. Such a medium is known as an optically denser medium. Thus optically denser medium is
that medium through which light travels slow.
The refraction of light takes place because of the speed of light
changes when the light goes from one medium to another medium.
Laws of refraction
- The incident ray, refracted ray, and the normal to the surface separating the two media all lie in the same plane.
- The ratio of the sine of incident angle (`\anglei`) to the sine of the refracted angle (`\angler`) is constant for a pair of two media.
`\frac{\sin i}{\sin r}` = Cosntant
The constant is known as the refractive index of the medium. The Refractive index is denoted by `n`.
The Refractive index of the second medium with respect to the first medium is denoted by `n_21`.
`\frac{\sin i}{\sin
r}` = `n_21`
This is also known as
Snell's law as it was stated by
Prof. Willebroad Snell (Dutch mathematician and astronomer).
Refractive Index
A ray of light that travels obliquely from one transparent medium into another will change its direction in the second medium. The extent of the change in direction that takes place in a given pair of media may be expressed in terms of the refractive index, the “constant”.
The refractive index can be linked to an important physical quantity, the relative speed of propagation of light in different media. It turns out that light propagates with different speeds in different media. Light travels fastest in vacuum with speed of `3×10^8 m s^{–1}`. In the air, the speed of light is only marginally less, compared to that in vacuum. It reduces considerably in glass or water. The value of the refractive index for a given pair of media depends upon the speed of light in the two media.
➤The refractive index of a transparent medium is the ratio of the speed of light in a vacuum to that in the medium.
Types of Refractive Index
- Relative Refractive Index
- Absolute Refractive Index
1. Relative Refractive Index
Consider a ray of light travelling from medium 1 into medium 2, as shown in Fig.
Let `v_1` be the speed of light in medium 1 and `v_2` be the speed of light in medium 2. The refractive index of medium 2 with respect to medium 1 is given by the ratio of the speed of light in medium 1 and the speed of light in medium 2. This is usually represented by the symbol `n_21`. This can be expressed in an equation form as
By the same argument, the refractive index of medium 1 with respect to medium 2 is represented as `n_12`. It is given by
2. Absolute Refractive Index
If medium 1 is vacuum or air, then the refractive index of medium 2 is considered with respect to vacuum. This is called the absolute refractive index of the medium. It is simply represented as `n_2`.
If `c` is the speed of light in air and `v` is the speed of light in the medium, then, the refractive index of the medium `n_m` is given by
➤ The absolute refractive index of a medium is simply called its refractive index.
Absolute refractive index of some material media
From the Table, you can know that the refractive index of water, `n_w = 1.33`. This means that the ratio of the speed of light in air and the speed of light in water is equal to 1.33. Similarly, the refractive index of crown glass, `n_g =1.52.`
Refraction by Spherical Lenses
Lens
A transparent material bound by two surfaces, of which one or both surfaces are spherical, forms a lens.
Convex lens
A lens may have two spherical surfaces, bulging outwards. Such a lens is called a double convex lens. It is simply called a convex lens. It is thicker in the middle as compared to the edges. Convex lens converges light rays as shown in Fig. (a). Hence convex lenses are also called converging lenses.
A double concave lens is bounded by two spherical surfaces, curved inwards. It is thicker at the edges than at the middle. Such lenses diverge light rays as shown in Fig.(b). Such lenses are also called diverging lenses. A double concave lens is simply called a concave lens.
➤A lens, either a convex lens or a concave lens, has two spherical surfaces. Each of these surfaces forms a part of a sphere.
Centres of Curvature of Lens
The centres of these spheres are called centres of curvature of the lens. The centre of curvature of a lens is usually represented by the letter C. Since there are two centres of curvature, we may represent them as `C_1` and `C_2`.
Principal axis
An imaginary straight line passing through the two centres of curvature of a lens is called its principal axis.
Optical centre
The central point of a lens is its optical centre. It is usually represented by the letter O. A ray of light through the optical centre of a lens passes without suffering any deviation.
Principal focus of the lens (Convex lens)
These rays, after refraction from the lens, are converging to a point on the principal axis. This point on the principal axis is called the principal focus of the lens.
Principal focus of the lens (Concave lens)
These rays, after refraction from the lens, are appearing to diverge from a point on the principal axis. This point on the principal axis is called the principal focus of the concave lens.
➤However, a lens has two principal foci. They are represented by `F_1` and `F_2`. The distance of the principal focus from the optical centre of a lens is called its focal length. The letter `f` is used to represent the focal length.
Ray Diagrams
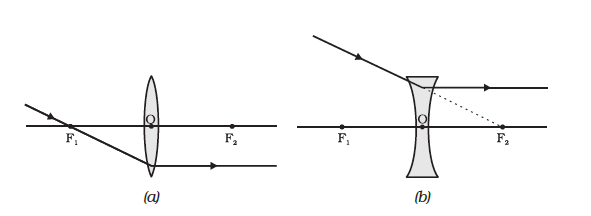
1. A ray of light from the object, parallel to the principal axis, after refraction from a convex lens, passes through the principal focus on the other side of the lens, as shown in Fig. (a). In the case of a concave lens, the ray appears to diverge from the principal focus located on the same side of the lens.
2. A ray of light passing through a principal focus, after refraction from a convex lens, will emerge parallel to the principal axis. This is shown in Fig.(a). A ray of light appearing to meet at the principal focus of a concave lens, after refraction, will emerge parallel to the principal axis.
3. A ray of light passing through the optical centre of a lens will emerge without any deviation. This is illustrated in Fig.(a) and Fig.(b).
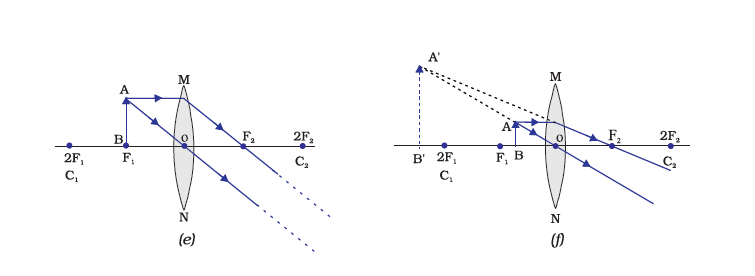
The ray diagrams for the image formation in a convex lens
Nature, position, and relative size of the image formed by a convex lens for various positions of the object
The ray diagrams for the image formation in a concave lens
Nature, position, and relative size of the image formed by a concave lens for various positions of the object
Sign convention for spherical lenses
According to the convention, the focal length of a convex lens is positive and that of a concave lens is negative. You must take care to apply appropriate signs for the values of `u, v, f`, object height `h`, and image height `h^'`.
Lens formula
`1/v - 1/u = 1/f`
object-distance `(u)`, image-distance `(v)` and the focal length `(f )`.
Magnification
The magnification produced by a spherical lens is the ratio of the height of the image (`h^'`) to the height of the object (`h`). It is represented by the letter `m`.
`m = h^'/h`
Magnification produced by a lens is also related to the object-distance `u`, and the image-distance `v`. This relationship is given by
`m = h^'/h = v/u`
Power of a lens
Power of a lens is the reciprocal of its focal length. It is represented by the letter `P`. The SI unit of power of a lens is dioptre. It is denoted by the letter D. The power of a convex lens is positive and that of a concave lens is negative.
`P = 1/f`
1 dioptre of power of a lens
1 dioptre is the power of a lens whose focal length is 1 metre. 1D = `1m^{–1}`.
Power of a Combination of Lenses
If a number of lenses are placed in close contact, then the power of the combination of lenses is equal to the algebraic sum of the powers of individual lenses.
`P = P_1 + P_2 +` ....
`P = \sum_{i = 1}^n P_i`
References:
- NCERT Science Class 10
- Super Simplified Science Physics Class 10 (Dinesh)
- Physics class 10 (S.Chand)








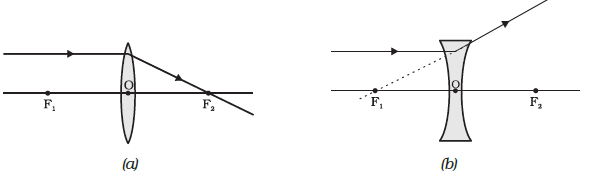





Very nice notes good 👍👍👍👍👍👍👍
ReplyDeleteThank you
DeleteVery very nice understanding note 👍👍👍👍👌👌👌👌💐💐
ReplyDeleteThank u jay sir
Excellent👍👍👍
ReplyDeleteThank you
Delete