Vector Algebra Class 12

📝 Vector Algebra

Some Basic Concepts

Scalars A quantity that has magnitude only is known as a scalar.

Examples

Mass, length, speed, time, temperature, density, etc.

Vectors A quantity that has magnitude as well as direction is called a vector.

Examples

Force, velocity, acceleration, etc.

Let `‘l’` be any straight line in-plane or three-dimensional space. This line can be given two directions by means of arrowheads. A line with one of these directions prescribed is called a directed line

Now observe that if we restrict line `l` to the line segment AB, then a magnitude is prescribed on the line `l` with one of the two directions, so that we obtain a directed line segment (Fig iii ). Thus, a directed line segment has magnitude as well as direction.

➤ A quantity that has magnitude, as well as direction, is called a vector.

Notice that a directed line segment is a vector (Fig iii), denoted as `\vec{AB}` or simply as `\vec {a}`, and read as ‘vector `\vec{AB}` ’ or 'vector `\vec {a}`'.

Point A from where the vector `\vec{AB}` starts is called its initial point, and point B where it ends is called its terminal point. The distance between the initial and terminal points of a vector is called the magnitude (or length) of the vector, denoted as | `\vec{AB}` |, or | `\vec {a}` |, or a. The arrow indicates the direction of the vector.

Types of Vectors

Zero Vector A vector whose initial and terminal points coincide, is called a zero vector (or null vector), and denoted as. A zero vector can not be assigned a definite direction as it has zero magnitude.

The vectors `\vec (A A)` represent the zero vector

Unit Vector A vector whose magnitude is unity (i.e., 1 unit) is called a unit vector. The unit vector in the direction of a given vector is denoted by `\hat a`.

`\hat a = frac {\vec a}{|\vec a |}`

Coinitial Vectors Two or more vectors having the same initial point are called coinitial vectors

Collinear Vectors Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.

Equal Vectors Two vectors `\vec a` and `\vec b` are said to be equal, if they have the same magnitude and direction regardless of the positions of their initial points, and written as `\vec a = \vec b`

Negative of a Vector A vector whose magnitude is the same as that of a given vector (say, `\vec {A B}`), but direction is opposite to that of it, is called negative of the given vector. For example, vector `\vec {BA}` is negative of the vector `\vec {AB}`.

Position Vector

Fig (i), consider a point `P` in space, having coordinates `(x, y, z)` with respect to the origin `O (0, 0, 0).` Then, the vector `\vec{OP}` having `O` and `P` as its initial and terminal points, respectively, is called the position vector of the point `P` with respect to `O. `

The magnitude of `\vec{OP} ( \vec{r})`

`|\vec{OP}| = sqrt{x^2 + y^2 + z^2}`

Fig (ii), in practice, the position vectors of points `A, B, C,` etc., with respect to the origin `O` are denoted by `\vec a , \vec b, \vec c`

Components of a Vector

Let `O` be the origin and let `P( x, y, z)` be any point in space. Let `\hat i, \hat j, \hat k` be the unit vectors along the `x `-axis, `y`-axis and `z`- axis respectively.

Let the position vector `\vec {OP}` be `\vec r`.

Then,

`\vec r = (x \hat i +y \hat j + z \hat k)`

This form of the vector is called its component form.

Here, `x, y, z` are called the scalar components of `\vecr` and `x \hat i, y \hat j, z \hat k` are called its vector components.

Magnitude of `\vec r`

`|\vec r| = | x \hat i + y \hat j + z \hat k | = sqrt{x^2 + y^2 + z^2}`

Direction Ratios & Direction Cosines of a Vector

Let a vector `\vec r = a \hat i + b \hat j +c \hat k`

Then, number `a,b,c` are called the direction ratios of `\vec r`

Direction cosines of `\vec r` are:

`frac{a}{\sqrt{a^2 +b^2 + c^2}}, frac{b}{\sqrt{a^2 +b^2 + c^2}}` and `frac{c}{\sqrt{a^2 +b^2 + c^2}}`

👉 Direction cosines of the vector `\vec r` , are usually denoted by `l, m` and `n`, respectively.

👉 The magnitude `r`, direction ratios `(a, b, c)` and direction cosines `(l, m, n)` of any vector are related as:

` l = a/r, m = b/r, n = c/r`

👉 `l^2 + m^2 + n^2 = 1`

Remarks

👉 Two vectors `\vec a and \vec b` are collinear

`⇔ \vec b = \lambda \vec a, \lamda \ne 0`

👉 If it is given that `l, m, n` are direction cosines of a vector, then `(l \hat i + m \hat j + n \hat k)` is the unit vector in the direction of that vector,.

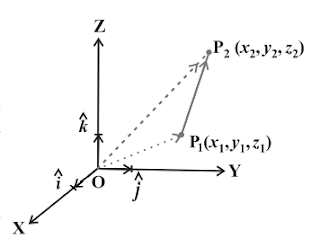
Vector joining two points

If `P_1 (x_1 , y_1 , z_1 )` and `P_2 (x_2 , y_2 , z_2 )` are any two points, then the vector joining `P_1` and `P_2` is the vector `vec{P_1 P_2}`

Joining the points `P_1` and `P_2` with the origin `O`, and applying triangle law, from the `\triangle OP_1 P_2` , we have

`\vec {OP_1} + \vec {P_1P_2} = \vec {OP_2}`

Section formula

The position vector of a point `R` dividing a line segment joining the points `P` and `Q` whose position vectors are `\vec a` and `\vec b` are respectively, in the ratio `m: n`

(i) internally, is given by `\frac {m \vec b +n \vec a}{m +n}`

(ii) externally, is given by `\frac {m \vec b - n \vec a}{m - n}`

Scalar (or dot) product of two vectors

The scalar product of two nonzero vectors, `\vec a` and `\vec b` denoted by `\vec a . \vec b`, is defined as

`\vec a . \vec b = |\vec a| |\vec b| \cos \theta `

where, `\theta` is the angle between `\vec a` and `\vec b`, `0 \leq \theta \leq \pi`

Observations

👉 `\vec a . \vec b` is a real number.

👉 Let `\vec a` and `vec b` be two nonzero vectors, then

`\vec a . \vec b = 0 ⇔ \vec a ⟂ vec b`

👉 If `θ = 0`, then `\vec a . \vec b = |\vec a| |\vec b|`

In particular, `\vec a . \vec a = |\vec a|^2`, as `θ` in this case is `0`.

👉 If either `\vec a = 0` or `\vec b = 0` then `θ` is not defined, and in this case, we define

`\vec a . \vec b = 0`

👉 For mutually ⟂ unit vectors `\hat i , \hat j` and `\hat k` , we have

`\hat i .\hat i = \hat j .\hat j = \hat k. \hat k = 1`

`\hat i . \hat j = \hat j . hat k = \hat k . hat i = 0`

👉 The angle between two nonzero vectors `\vec a` and `\vec b`

`cos θ = \frac{\vec a . \vec b}{ |\vec a| |\vec b|}`

` ⇒ θ = cos^{-1} (\frac{\vec a . \vec b}{ |\vec a| |\vec b|})`

Cauchy-Schwartz inequality

Prove that `|\vec a · \vec b| ≤ |\vec a||\vec b|`

Proof:

If `\vec a = 0 = \vec b`, then `|\vec a · \vec b| = |\vec a||\vec b|`

Let `\vec a ≠ 0 ≠ \vec b`, then

`\vec a · \vec b = |\vec a||\vec b| \cos \theta`

`⇒ |\vec a · \vec b| = |\vec a||\vec b| |\cos \theta|`

`⇒ \frac{|\vec a · \vec b|}{ |\vec a||\vec b| } = |\cos \theta| ≤ 1`

`⇒ |\vec a · \vec b| ≤ |\vec a||\vec b|`

Hence, `|\vec a · \vec b| ≤ |\vec a||\vec b|`

👉If `\vec a` and `\vec b` represent the adjacent sides of a triangle then its area is given as

`\frac{1}{2}|\vec a \times \vec b|`

`ar(\Delta ABC) = 1/2 AB · CD`

`AB = |\vec b|` and `CD = |\vec a| sin \theta`