Class 10 Maths Chapter 6 Triangles

  📝Class 10 Maths Chapter 6 Triangles

Concept of Similarity

Congruent figures 

Two geometric figures having the same shape and size are known as congruent figures. 

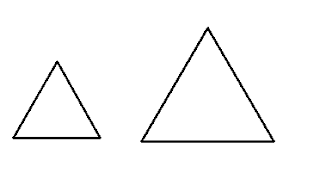
Similar figures

Two figures having the same shape but not necessarily the same size are called similar figures.

➤ All the congruent figures are similar but the converse is not true.

Example 1

Any two line segments are always similar but they need not be congruent. They are congruent if their lengths are equal.

Example 2

Any two circles are similar but not necessarily congruent. They are congruent if their radii are equal.

Example 3

(i) Any two squares are similar 

 (ii) Any two equilateral triangles are similar 

➤ Two polygons of the same number of sides are similar if 

(i) all the corresponding angles are equal  

(ii) all the corresponding sides are in the same ratio (or proportion).

(i)`angleA = angleP` = 105°, `angleB = angleQ` = 100°, `angleC = angleR` = 70°, `angleD = angleS` = 85°

(ii) `frac{AB}{PQ} = 1.5/3.0 =  frac{BC}{QR}= 2.5/5.0 = frac{CD}{RS} = 2.4/4.8 =   frac{DA}{SP} = 2.1/4.2`

`therefore` ABCD  ~ PQRS

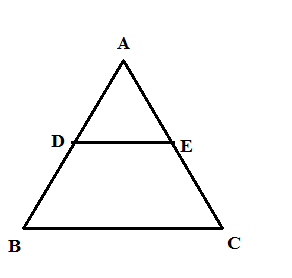
Basic Proportionality Theorem (Thales's Theorem)

➤Theorem: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio

If `DE ∥ BC`

then, `frac{AD}{DB} = frac{AE}{EC}` 

Summary

If in  a `triangleABC`,  `DE ∥ BC` and intersect AB in D and AC in E, then we have

(i) `frac{AD}{DB} = frac{AE}{EC}`

(ii) `frac{DB}{AD} = frac{EC}{AE}`

(iii) `frac{AB}{AD} = frac{AC}{AE}`

(iv) `frac{AD}{AB} = frac{AE}{AC}`

(v)  `frac{AB}{DB} = frac{AC}{EC}`

(vi) `frac{DB}{AB} = frac{EC}{AC}`

Converse of Basic Proportionality Theorem (Thales's Theorem)

➤Theorem: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

If `frac{AD}{DB} = frac{AE}{EC}`

then, `DE ∥ BC`

Criteria for Similarity of Triangles

Two triangles  `triangleABC and triangleDEF` are similar if 

(i) `angleA = angleD, angleB = angleE, angleC = angleF`

(ii) `frac{AB}{DE} = frac{BC}{EF} = frac{CA}{FD}`

➤Theorem: If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar. (AAA-similarity).

If `angleA = angleD, angleB = angleE, angleC = angleF`, 

then `triangleABC ∼ triangleDEF`.

Given `triangleABC` and `triangleDEF, angleA = angleD, angleB = angleE, angleC = angleF` 

To prove `triangleABC` ∼ `triangleDEF`

Construction  Cut DP = AB, DQ = AC

Proof   In `triangleABC` and `triangleDPQ`

AB = DP (by constuction)

AC = DQ (by construction)

`angleA = angleD` (Given)

`∴ triangleABC ≅ triangleDPQ` (by SAS-congruence)

`⇒ angleB = angleP` 

`⇒ angleE = angleP  [ ∵angleB = angleE (given)]`

`∴ PQ ∥ EF`  (∵ corresponding `∠s` are equal)

`⇒ frac{DP}{DE} = frac{DQ}{DF}` (by BPT)

`⇒ frac{AB}{DE} = frac{AC}{DF}  (∵ DP = AB, DQ = AC )`

Similarly, `frac{AB}{DE} = frac{BC]{EF}`

∴  `frac{AB}{DE} = frac{BC]{EF} = frac{CA}{FD}`

Thus `angleA = angleD, angleB = angleE, angleC = angleF` 

and  `frac{AB}{DE} = frac{BC]{EF} = frac{CA}{FD}`

Hence,  `triangleABC` ∼ `triangleDEF`

Remark: Two `triangle`s are similar `⇔` they are equiangular. 

Work in progress ....

➤Theorem: If two angles of one triangle are respectively equal to two angles of another triangle then two triangles are similar. (AA-similarity).

If `angleA = angleD, angleB = angleE`,

then `triangleABC ∼ triangleDEF`.

➤ Theorem: If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar. (SSS-similarity).

If `frac{AB}{DE} = frac{BC}{EF} = frac{CA}{FD}`, 

then  `triangleABC ∼ triangleDEF`.

Given `frac{AB}{DE} = frac{BC}{EF} = frac{CA}{FD}`, 

To prove  `triangleABC` ∼ `triangleDEF`

Construction  Cut DP = AB, DQ = AC

➤ Theorem: If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar. (SAS-similarity).

If  `angleA = angleD` and `frac{AB}{DE} = frac{AC}{DF}`,

 then `triangleABC ∼ triangleDEF`

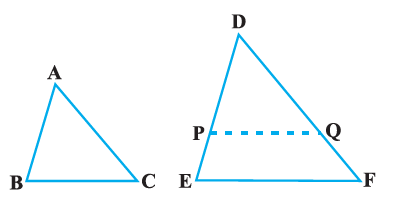
➤ Theorem: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

`frac {ar(triangleABC)}{ar(trianglePQR)} = (frac{AB}{PQ})^2 = (frac{BC}{QR})^2= (frac{CA}{RP})^2`