Functions
Function
● Let `X` and `Y` be two nonempty sets. Then, a relation `f` from `X` to `Y` is called a function, if every element in `X` has a unique image in `Y`, and we write, `f: X \rightarrow Y`.
Thus, a relation `f` from `X` to `Y` is a function, if dom `(f) = X` and no two distinct ordered pairs in `f` have the same first coordinate.
If `(x,y) \in f`, we write `f(x) = y`
Here, `y` is called the image of `x` under `f` and `x` is called the pre-image of `y`.
If `f: X \rightarrow Y` then dom`(f) = X` and range `(f) \subseteq Y`.
Also, `Y` is called the co-domain of `f`.
● dom `(f) = {x: (x,y) \in f} = X`
● range `(f) = {y: (x,y) \in f} \subseteq Y`
● co-domain `(f) = Y`
Real Function
● A function which has either `R` or one of its subsets as its range is called
a real-valued function. Further, if its domain is also either `\R` or a subset of `R`, it is
called a real function.
Types of Functions
- Identity function
- Constant function
- Polynomial function
- Rational function
- Modulus function
- Signum function
- Greatest integer function
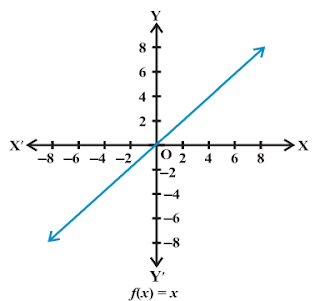
1. Identity function
The function `f : R → R` defined by `y = f (x) = x, forall x ∈ R` is called the
identity function.
The graph is a straight line as
shown in Fig. It passes through the origin.
Dom `(f )= R`
Range `(f) = R`
2. Constant function
The function `f : R → R` defined by `y = f (x) = c, forallx ∈ R`,
where `c` is a constant `∈ R`, is a constant function.
Dom `(f) = R`
Range `(f )= {C}`
A function `f : R → R` is said to be polynomial function if `forall x in R, y = f (x) = a_0
+ a_1
x + a_2
x ^2 + a_n
x^ n` , where `n` is a non-negative
integer and `a_0
, a_1
, a_2
,...,a_n∈R`.
4. Rational functions
Rational functions are functions of the type `\frac{f(x)}{g(x)}`, where `f(x)` and `g(x)` are
polynomial functions of `x` defined in a domain, where `g(x) ≠ 0`.
5. Modulus function
The function `f: R→R` defined by `f(x) = |x| forall x ∈R` is called modulus function.
`therefore` dom`(f) = R`
range `(f) = [0, ∞)`
Algebra of real functions
(i) Addition of two real functions
(ii) Subtraction of a real function from another
(iii) Multiplication by a scalar
(iv) Multiplication of two real functions
(v) Quotient of two real functions
(i) Addition of two real functions
Let `f : X → R` and `g : X → R` be any two real
functions, where `X ⊂ R`.
Then, we define `(f + g): X → R` by `(f + g) (x) = f (x) + g (x), \forall x ∈ X`.
(ii) Subtraction of a real function from another
Let `f : X → R` and `g: X → R` be
any two real functions, where `X ⊂ R`.
Then, we define `(f – g) : X→R` by `(f–g) (x) = f(x) –g(x), \forall x ∈ X`.
References:
- NCERT Mathematics Class 11
- NCERT Exemplar Class 11

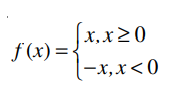

“Wherever you go, no matter what the weather, always bring your own sunshine.” “If you want light to come into your life, you need to stand where it is shining.” “Success is the sum of small efforts repeated day in and day out.” “Happiness is the only thing that multiplies when you share it.”
ReplyDeleteNice
ReplyDeleteGood ,keep it up............
ReplyDelete